.(本小题满分14分)电视台应某企业之约播放两套连续剧.其中,连续剧甲每次播放时间为80min,其中广告时间为1min,收视观众为60万;连续剧乙每次播放时间为40min,其中广告时间为1min,收视观众为20万.已知此企业与电视台达成协议,要求电视台每周至少播放6min广告,而电视台每周只能为该企业提供不多于320min的节目时间(此时间不包含广告).如果你是电视台的制片人,电视台每周播映两套连续剧各多少次,才能获得最高的收视率?
(本小题满分8分)已知椭圆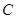 :
: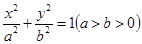 的一个焦点与抛物线
的一个焦点与抛物线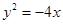 的焦点相同,
的焦点相同,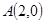 在椭圆上,过椭圆的右焦点
在椭圆上,过椭圆的右焦点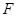 作斜率为
作斜率为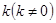 的直线
的直线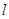 与椭圆交于
与椭圆交于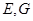 两点,直线
两点,直线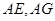 分别交直线
分别交直线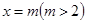 于点
于点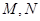 ,线段
,线段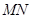 的中点为
的中点为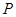 ,记直线
,记直线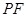 的斜率为
的斜率为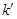 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)求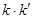 的取值范围。
的取值范围。
(本小题满分8分)已知数列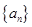 的首项为
的首项为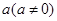 ,前
,前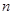 项和为
项和为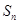 ,且有
,且有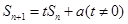 ,
,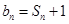 .
.
(Ⅰ)求证:数列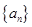 是等比数列;
是等比数列;
(Ⅱ)当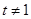 时,若
时,若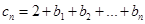 ,求能够使数列
,求能够使数列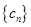 为等比数列的所有数对
为等比数列的所有数对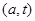
(本小题满分8分)如图,在四棱锥P−ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.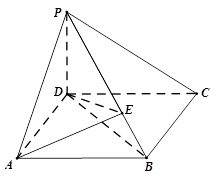
(Ⅰ)求证:平面PAD⊥平面PBD;
(Ⅱ)若PD=AD=1, ,求二面角P−AD−E的余弦值.
,求二面角P−AD−E的余弦值.
(本小题满分7分)在△ABC中,内角A、B、C对应的三边长分别为a,b,c,且满足c(acosB− b)=a2−b2.
b)=a2−b2.
(Ⅰ)求角A;
(Ⅱ)若a=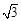 ,求b+c的取值范围.
,求b+c的取值范围.
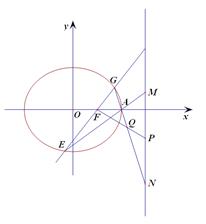
在直角坐标系 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线 相切.
相切.
(1)求圆 的方程;
的方程;
(2)圆 与
与 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点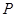 使
使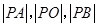 成等比数列,求
成等比数列,求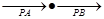 的取值范围.
的取值范围.