(本小题满分12分)
某学校高一年级为了了解学生在一次数学考试中的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分是100分)作为样本(样本容量为a)进行统计,按照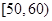 ,
, ,
,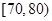 ,
, ,
,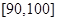 的分组作出如图甲所示的频率分布直方图和图乙所示的样本分数的茎叶图(图乙中仅列出了得分在
的分组作出如图甲所示的频率分布直方图和图乙所示的样本分数的茎叶图(图乙中仅列出了得分在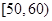 ,
,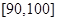 的数据).
的数据).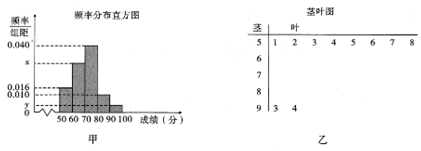
(Ⅰ)求样本容量n和频率分布直方图中x,y的值;
(Ⅱ)在选取的样本中,从考试成绩是80分以上(含80分)的同学中随机抽取3名同学为其他同学作交流,设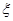 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在 的学生个数,求
的学生个数,求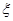 的分布列及其数学期望.
的分布列及其数学期望.
(本小题满分12分)如图,长方体 中,
中, ,
, ,点E是AB的中点.
,点E是AB的中点.
(Ⅰ)求证: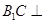 平面
平面 ;
;
(Ⅱ)求二面角 .
.
(本小题满分12分)已知函数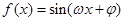
 的一系列对应值如下表:
的一系列对应值如下表:
(Ⅰ)求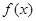 的解析式;
的解析式;
(Ⅱ)在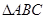 中,若
中,若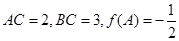 ,求
,求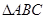 的面积.
的面积.
(本小题满分14分)已知函数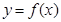 ,
,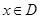 ,设曲线
,设曲线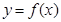 在点
在点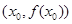 处的切线方程为
处的切线方程为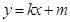 .如果对任意的
.如果对任意的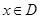 ,均有:
,均有:
①当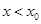 时,
时,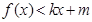 ;
;
②当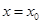 时,
时,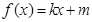 ;
;
③当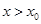 时,
时,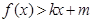 ,
,
则称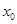 为函数
为函数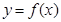 的一个“ʃ-点”.
的一个“ʃ-点”.
(Ⅰ)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
①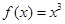 ; ②
; ②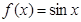 .(只需写出结论)
.(只需写出结论)
(Ⅱ)设函数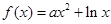 .
.
(ⅰ)若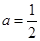 ,证明:
,证明: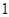 是函数
是函数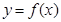 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数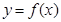 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出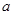 的取值范围.
的取值范围.
(本小题满分13分)已知数列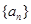 满足
满足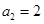 ,
,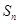 为其前
为其前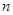 项和,且
项和,且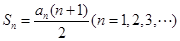 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: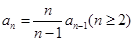 ;
;
(Ⅲ)判断数列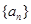 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.