(本小题满分12分)已知
(1)讨论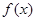 的单调性,
的单调性,
(2)当 时,若对于任意
时,若对于任意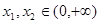 ,都有
,都有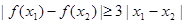 ,求
,求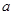 的取值
的取值
范围.
已知函数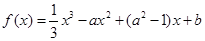 (
(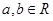 ),其图像在点(1,
),其图像在点(1,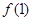 )处的切线方程为
)处的切线方程为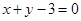 .
.
(1)求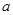 ,
,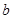 的值;
的值;
(2)求函数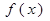 的单调区间和极值;
的单调区间和极值;
(3)求函数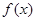 在区间[-2,5]上的最大值.
在区间[-2,5]上的最大值.
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
根据以上数据建立一个2×2的列联表;
能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据: ,其中
,其中 .
.
| K2≥k0 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知复数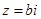 (
(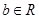 ),
),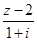 是实数,
是实数,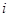 是虚数单位.
是虚数单位.
(1)求复数z;
(2)若复数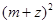 所表示的点在第一象限,求实数m的取值范围.
所表示的点在第一象限,求实数m的取值范围.
已知函数f(x)= -2alnx(a>0)
-2alnx(a>0)
(I)求函数f(x)的单调区间和最小值.
(II)若方程f(x)=2ax有唯一解,求实数a的值.
设F(x)=3a +2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
+2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
求证:a>0,且—2< <—1.
<—1.