已知正项数列 的前
的前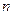 项和
项和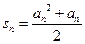 ,
,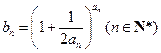 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)定理:若函数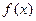 在区间D上是凹函数,且
在区间D上是凹函数,且 存在,则当
存在,则当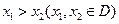 时,总有
时,总有 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数 是
是 上的凹函数,判断
上的凹函数,判断 与
与 的大小;
的大小;
(Ⅲ)求证: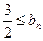 .
.
如图,四边形ABCD为梯形,AB∥CD, 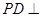 平面ABCD,
平面ABCD, ,
, ,E为BC中点。
,E为BC中点。
(1)求证:平面 平面PDE;
平面PDE;
(2)线段PC上是否存在一点F,使PA//平面BDF?若存在,请找出具体位置,并进行证明;若不存在,请分析说明理由.
为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前 次考试的数学成绩
次考试的数学成绩 、物理成绩
、物理成绩 进行分析.下面是该生
进行分析.下面是该生 次考试的成绩.
次考试的成绩.
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的理由;
(2)已知该生的物理成绩 与数学成绩
与数学成绩 是线性相关的,若该生的物理成绩达到
是线性相关的,若该生的物理成绩达到 分,请你估计他的数学成绩大约是多少?
分,请你估计他的数学成绩大约是多少?
(已知88 94+83
94+83 91+117
91+117 108+92
108+92 96+108
96+108 104+100
104+100 101+112
101+112 106=70497,
106=70497, )
)
(参考公式: ,
, )
)
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为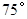 ,
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,
,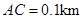 .试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到
.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到
0.01km,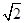
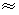 1.414,
1.414,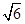
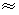 2.449).
2.449).
设数列{an}满足a1=2,an+1-an=3·4n(n∈N*).
(1)求数列{an}的通项公式;
(2)令bn=n+an,求数列{bn}的前n项和Sn.
在△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面积为2 ,求b,c.
,求b,c.