【必做题】(本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是‘‘海宝”,即可获奖,否则,均为不获奖.卡片用后后放同盒子,下一位参加者继续重复进行。
(I)有三人参加抽奖,要使至少一人获奖的概率不低于 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(2)若有四张“海宝”卡,现有甲乙丙丁四人依次抽奖.用 表示获奖的人数,求
表示获奖的人数,求 的分布列及E
的分布列及E 的值.
的值.
(本小题满分12分)已知数列 中,
中, ,且当
,且当 时,
时, .
.
(Ⅰ)求证:数列 为等比数列.
为等比数列.
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知一个空间几何体的直观图和三视图(尺寸如图所示).
(Ⅰ)设点 为棱
为棱 中点,求证:
中点,求证: 平面
平面 ;
;
(Ⅱ)线段 上是否存在一点
上是否存在一点 ,使得直线
,使得直线 与平面
与平面 所成角的正弦值等于
所成角的正弦值等于 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本小题满分12分)调查表明,中年人的成就感与收入、学历、职业的满意度的指标有极强的相关性.现将这三项的满意度指标分别记为 ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标 的值评定中年人的成就感等级:若
的值评定中年人的成就感等级:若 ,则成就感为一级;若
,则成就感为一级;若 ,则成就感为二级;若
,则成就感为二级;若 ,则成就感为三级.为了了解目前某群体中年人的成就感情况,研究人员随机采访了该群体的10名中年人,得到如下结果:
,则成就感为三级.为了了解目前某群体中年人的成就感情况,研究人员随机采访了该群体的10名中年人,得到如下结果:
| 人员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 人员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(Ⅰ)在这10名被采访者中任取两人,求这两人的职业满意度指标 相同的概率;
相同的概率;
(Ⅱ)从成就感等级是一级的被采访者中任取一人,其综合指标为 ,从成就感等
,从成就感等
级不是一级的被采访者中任取一人,其综合指标为 ,记随机变量
,记随机变量 ,求
,求 的分布列及其数学期望.
的分布列及其数学期望.
(本小题满分12分)已知函数 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 的内角
的内角 所对的边分别是
所对的边分别是 .若
.若
 ,求角
,求角 的大小.
的大小.
(本小题满分14分)已知函数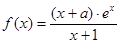 (
(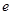 为自然对数的底数),曲线
为自然对数的底数),曲线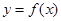 在
在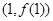 处的切线与直线
处的切线与直线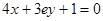 互相垂直.
互相垂直.
(Ⅰ)求实数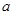 的值;
的值;
(Ⅱ)若对任意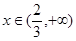 ,
, 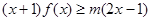 恒成立,求实数
恒成立,求实数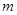 的取值范围;
的取值范围;
(Ⅲ)设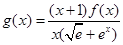 ,
,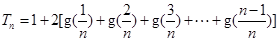
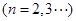 .问:是否存在正常数
.问:是否存在正常数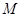 ,对任意给定的正整数
,对任意给定的正整数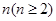 ,都有
,都有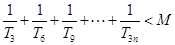 成立?若存在,求
成立?若存在,求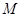 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.