已知不等式的解集为P。
(1)若P≠Ø,求实数a的取值范围;
(2)是否存在实数a,使P∩Z={6,8},若存在,求出a的取值范围;若不存在,请说明理由。
一几何体的表面展开图如右图,则这个几何体是哪一种几何体?选择适当的角度,画出它水平放置时的直观图与三视图.并计算该几何体的体积.
如右图所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为,设这条最短路线与CC1的交点为N.求: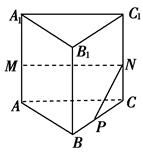
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.
点P(x0,y0)在椭圆+=1(a>b>0)上,x0=acos β,y0=bsin β,0<β<.直线l2与直线l1:x+y=1垂直,O为坐标原点,直线OP的倾斜角为α,直线l2的倾斜角为γ.
(1)证明:点P是椭圆+=1与直线l1的唯一交点;
(2)证明:tan α,tan β,tan γ构成等比数列.
已知直线x-2y+2=0经过椭圆C:+=1(a>b>0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS、BS与直线l:x=分别交于M、N两点.
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上是否存在这样的点T,使得△TSB的面积为?若存在,确定点T的个数,若不存在,说明理由.
已知n∈N*,求证:··……>.