我们用部分自然数构造如下的数表:用aij(i≥j)表示第i行第j个数(i、j为正整数),使ail=aii="i" ;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第n(n为正整数)行中各数之和为bn.
(1)试写出b2一2b1;,b3-2b2,b4-2b3,b5-2b4,并推测bn+1和bn的关系(无需证明);
(2)证明数列{bn+2}是等比数列,并求数列{bn}的通项公式bn;
(3)数列{ bn}中是否存在不同的三项bp,bq,br(p,q,r为正整数)恰好成等差数列?若存在求出P,q,r的关系;若不存在,请说明理由.
 |
(本小题共13分)
已知每项均是正整数的数列 :
: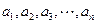 ,其中等于
,其中等于 的项有
的项有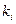 个
个 ,
,
设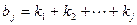
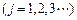 ,
,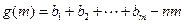
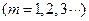 .
.
(Ⅰ)设数列 ,求
,求 ;
;
(Ⅱ)若数列 满足
满足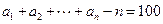 ,求函数
,求函数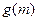 的最小值.
的最小值.
(本小题共14分)
已知椭圆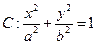
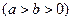 经过点
经过点 其离心率为
其离心率为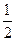 .
.
(Ⅰ) 求椭圆
求椭圆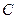 的方程;
的方程;
(Ⅱ)设直线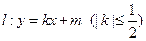 与椭圆
与椭圆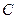 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆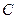 上,
上,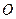 为坐标原点.求
为坐标原点.求 的取值范围.
的取值范围.
(本小题共13分)
已知函数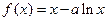 ,
,
(Ⅰ)若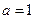 ,求函数
,求函数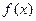 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若在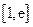 (
(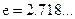 )上存在一点
)上存在一点 ,使得
,使得
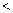
 成立,求
成立,求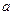 的取值范围
的取值范围
(本小题共13分)
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ)随机选取3件产品,其中一等品的件数记为 ,求
,求 的分布列;
的分布列;
(Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.
(本小题共14分)
在如图的多面体中, ⊥平面
⊥平面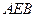 ,
,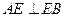 ,
, ,
, ,
, ,
, ,
,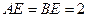 ,
, 是
是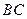 的
的 中点.
中点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: ;
;
(Ⅲ) 求二面角 的余弦值.
的余弦值.