(本小题共14分)
在如图的多面体中, ⊥平面
⊥平面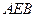 ,
,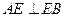 ,
, ,
, ,
, ,
, ,
,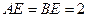 ,
, 是
是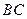 的
的 中点.
中点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: ;
;
(Ⅲ) 求二面角 的余弦值.
的余弦值.
设X~N(10,1).
(1)证明:P(1<X<2)=P(18<X<19);
(2)设P(X≤2)=a,求P(10<X<18).
工厂制造的某机械零件尺寸X服从正态分布N(4, ),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
设X~N(1,22),试求
(1)P(-1<X≤3);
(2)P(3<X≤5);
(3)P(X≥5).
标准正态分布的概率密度函数是P(x)= ·
· (x∈R).
(x∈R).
(1)求证:P(x)是偶函数;
(2)求P(x)的最大值;
(3)利用指数函数的性质说明P(x)的增减性.
若一个正态分布的概率密度函数是一个偶函数,且该函数的最大值为 .
.
(1)求该正态分布的概率密度函数的解析式;
(2)求正态总体在(-4,4]的概率.