(本小题满分16分)已知数列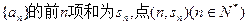 在函数
在函数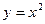 的图象上,数列
的图象上,数列 满足
满足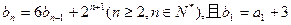 (1)求数列
(1)求数列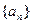 的通项公式;(2)证明列数
的通项公式;(2)证明列数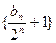 是等比数列,并求数列
是等比数列,并求数列 的通项公式;(3)设数列
的通项公式;(3)设数列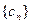 满足对任意的
满足对任意的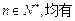
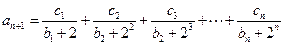 成立,
成立,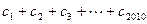 的值。
的值。
已知在四棱锥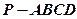 中,底面
中,底面 是矩形,且
是矩形,且 ,
,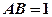 ,
, 平面
平面 ,
, 分别是线段
分别是线段 的中点。
的中点。
(Ⅰ)证明: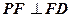 ;
;
(Ⅱ)判断并说明 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 。
。
如图四棱锥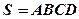 中,
中, ,
, ,
,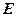 是
是 的中点,
的中点,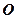 是底面正方形
是底面正方形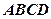 的中心,
的中心,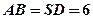 。
。
(Ⅰ)求证: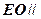 面
面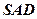 ;
;
(Ⅱ)求直线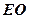 与平面
与平面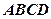 所成的角。
所成的角。
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图, 在直观图中,
在直观图中, 是
是 的中点,
的中点, 是
是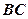 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证: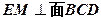 ;
;
(Ⅱ)求三棱锥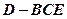 的体积。
的体积。
已知三棱锥 中,
中,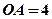 ,
, ,
, ,且
,且 两两垂直,
两两垂直, 是
是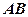 中点,
中点,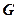 是
是 重心,现如图建立空间直角坐标系
重心,现如图建立空间直角坐标系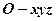 。
。
(Ⅰ)求点 和
和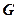 的坐标;
的坐标;
(Ⅱ)求异面直线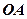 和
和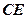 所成角的余弦值。
所成角的余弦值。
已知直线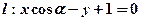 。
。
(Ⅰ)当 时,求直线
时,求直线 的斜率;
的斜率;
(Ⅱ)若直线
 的倾斜角为
的倾斜角为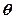 ,求
,求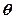 范围。
范围。