在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:
(1)乙连胜四局的概率;
(2)丙连胜三局的概率.
记函数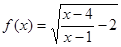 的定义域为
的定义域为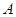 ,
,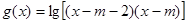 的定义域为
的定义域为 .若
.若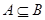 ,求实数
,求实数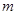 的取值范围.
的取值范围.
已知 为实数,数列
为实数,数列 满足
满足 ,当
,当 时,
时, ,
,
(Ⅰ) ;(5分)
;(5分)
(Ⅱ)证明:对于数列 ,一定存在
,一定存在 ,使
,使 ;(5分)
;(5分)
(Ⅲ)令 ,当
,当 时,求证:
时,求证: (6分)
(6分)
已知函数 ,
, ,(其中
,(其中 ),设
),设 .
.
(Ⅰ)当 时,试将
时,试将 表示成
表示成 的函数
的函数 ,并探究函数
,并探究函数 是否有极值;
是否有极值;
(Ⅱ)当 时,若存在
时,若存在 ,使
,使 成立,试求
成立,试求 的范围.
的范围.
已知圆 的方程为
的方程为 ,点
,点 是坐标原点.直线
是坐标原点.直线 与圆
与圆 交于
交于 两点.
两点.
(1)求 的取值范围;
的取值范围;
(2)设 是线段
是线段 上的点,且
上的点,且 .请将
.请将 表示为
表示为 的函数.
的函数.
如图,两座建筑物 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9 和15
和15 ,从建筑物
,从建筑物 的顶部
的顶部 看建筑物
看建筑物 的视角
的视角 .
.
⑴求 的长度;
的长度;
⑵在线段 上取一点
上取一点 点
点 与点
与点 不重合),从点
不重合),从点 看这两座建筑物的视角分别为
看这两座建筑物的视角分别为 问点
问点 在何处时,
在何处时, 最小?
最小?