已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.(1)求椭圆C的标准方程;
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.(1)求椭圆C的标准方程;
(2)若点P的坐标为(1,1),求证:直线PQ与圆 相切;
相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由. 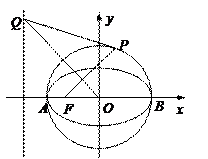
已知抛物线 的焦点F也是椭圆
的焦点F也是椭圆
 的一个焦点,
的一个焦点, 与
与 的公共弦长为
的公共弦长为 ,过点F的直线
,过点F的直线 与
与 相交于
相交于 两点,与
两点,与 相交于
相交于 两点,且
两点,且 与
与 同向.
同向.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)若 ,求直线
,求直线 的斜率.
的斜率.
设数列 的前
的前 项和为
项和为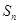 ,已知
,已知 ,且
,且
 .
.
(Ⅰ)证明: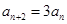 ;
;
(Ⅱ)求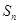 .
.
已知长方体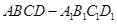 ,点
,点 为
为 的中点.
的中点.
(1)求证: 面
面 ;
;
(2)若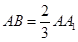 ,试问在线段
,试问在线段 上是否存在点
上是否存在点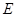 使得
使得
 ,若存在求出
,若存在求出 ,若不存在,说明理由.
,若不存在,说明理由.
某车间将10名技工平均分成甲.乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为 .
.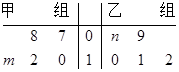
(1)分别求出 ,
,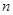 的值;
的值;
(2)分别求出甲.乙两组技工在单位时间内加工的合格零件的方差 和
和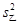 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲.乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差 ,其中
,其中 为数据
为数据 的平均数).
的平均数).
如图,在平面四边形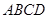 中,
中,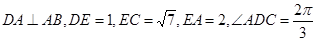 ,
,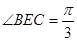
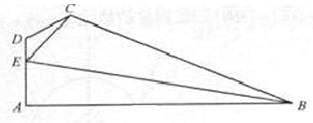
(1)求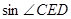 的值;
的值;
(2)求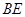 的长.
的长.