设函数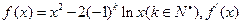 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{ }满足
}满足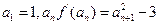 .证明:数列{
.证明:数列{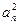 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有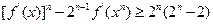 成立.
成立.
为了保护环境,某工厂在政府部门的支持下,进行技术改进: 把二氧化碳转化为某种化工产品,经测算,该处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似地表示为:
(吨)之间的函数关系可近似地表示为: , 且每处理一吨二氧化碳可得价值为
, 且每处理一吨二氧化碳可得价值为 万元的某种化工产品.
万元的某种化工产品.
(Ⅰ)当 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(Ⅱ) 当处理量为多少吨时,每吨的平均处理成本最少.
(本小题12分) 已知二次函数 与
与 轴有两个交点
轴有两个交点 和
和 ,若,且
,若,且
 .
.
(Ⅰ)求此二次函数的解析式
(Ⅱ)若 在闭区间
在闭区间 的最大值为
的最大值为 ,求
,求 的解析式及其最大值
的解析式及其最大值
(本小题满分12分)
设当 时,函数
时,函数 的值域为
的值域为 ,且当
,且当 时,恒有
时,恒有 ,求实数k的取值范围.
,求实数k的取值范围.
(本小题12分)
已知函数
(1)求 的最小正周期及其单调增区间.
的最小正周期及其单调增区间.
(2)当 时,求
时,求 的值域.
的值域.
已知集合A=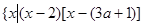
 ,集合B=
,集合B=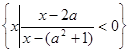 .
.
(1)当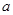 =2时,求
=2时,求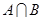 ;
;
(2)当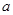
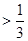 时,若元素
时,若元素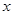
 是
是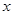
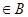 的必要条件,求实数
的必要条件,求实数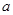 的取值范围.
的取值范围.