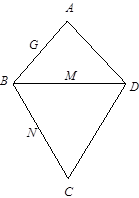如图,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB∶AD= ∶1,F是AB的中点.
∶1,F是AB的中点.
(1)求VC与平面ABCD所成的角;
(2)求二面角V-FC-B的度数;
(3)当V到平面ABCD的距离是3时,求B到平面VFC的距离.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点.
(1)求证:B1E⊥AD1;
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由;
(高考真题)如图,在三棱柱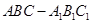 中,侧棱垂直于底面,
中,侧棱垂直于底面,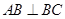 ,
,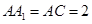 ,BC=1,
,BC=1,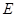 、
、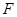 分别为
分别为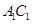 、
、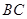 的中点.
的中点.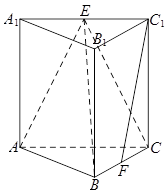
(1)求证:平面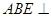 平面
平面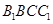 ;
;
(2)求证: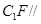 平面
平面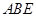 ;
;
(3)求三棱锥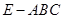 的体积.
的体积.
如图,已知四边形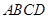 是正方形,
是正方形,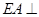 平面
平面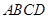 ,
,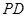 ∥
∥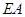 ,
,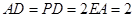 ,
,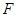 ,
,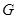 ,
,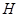 分别为
分别为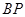 ,
,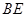 ,
,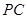 的中点.
的中点.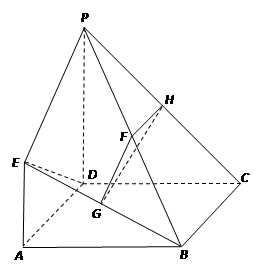
(Ⅰ)求证: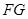 ∥平面
∥平面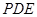 ;
;
(Ⅱ)求证:平面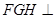 平面
平面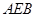 ;
;
(Ⅲ)(有点难度哦)在线段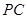 上是否存在一点
上是否存在一点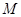 ,使
,使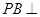 平面
平面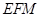 ?若存在,求出线段
?若存在,求出线段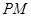 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.
(1)求证:DE∥平面ABC;
(2)求三棱锥E-BCD的体积.
如图,△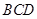 是等边三角形,
是等边三角形,  ,
, ,
, ,
,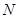 ,
,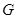 分别是
分别是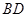 ,
,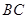 ,
,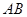 的中点,将△
的中点,将△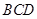 沿
沿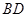 折叠到△
折叠到△ 的位置,使得
的位置,使得 .求证:平面
.求证:平面 平面
平面 ;
;