如图,已知四边形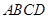 是正方形,
是正方形,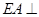 平面
平面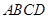 ,
,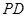 ∥
∥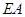 ,
,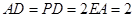 ,
,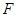 ,
,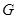 ,
,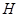 分别为
分别为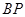 ,
,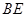 ,
,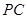 的中点.
的中点.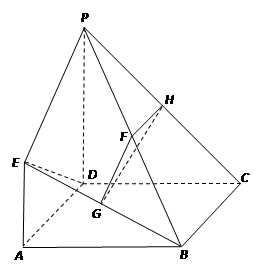
(Ⅰ)求证: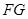 ∥平面
∥平面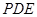 ;
;
(Ⅱ)求证:平面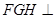 平面
平面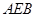 ;
;
(Ⅲ)(有点难度哦)在线段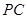 上是否存在一点
上是否存在一点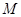 ,使
,使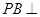 平面
平面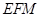 ?若存在,求出线段
?若存在,求出线段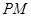 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
设椭圆M: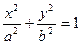 (a>b>0)的离心率为
(a>b>0)的离心率为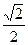 ,长轴长为
,长轴长为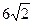 ,设过右焦点F倾斜角
,设过右焦点F倾斜角
为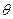 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | =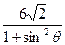 ;
;
(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C, D,求|AB| + |CD|的最小值。
D,求|AB| + |CD|的最小值。
已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP到点N,且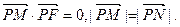
(Ⅰ)求动点N的轨迹方程;
(Ⅱ)直线l与动点N的轨迹交于A、B两点,若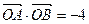 ,且
,且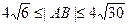 ,
,
求直线l的斜率k的取值范围.
双曲线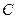 的中心在原点,右焦点为
的中心在原点,右焦点为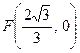 ,渐近线方程为
,渐近线方程为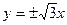 .
.
(Ⅰ)求双曲线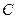 的方程;
的方程;
(Ⅱ)设直线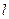 :
: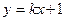 与双曲线
与双曲线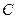 交于
交于 、
、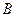 两点,问:当
两点,问:当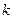 为何值时,以
为何值时,以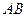 为直径的圆过原点。
为直径的圆过原点。
若圆C经过点 和
和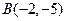 ,且圆心C在直线
,且圆心C在直线 上,求圆C的方程.
上,求圆C的方程.
已知命题p:方程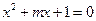 有两个不相等的实根;
有两个不相等的实根;
命题q:不等式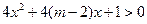 的解集为R;
的解集为R;
若p∨q为真,p∧q为假,求实数m的取值范围。