某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| 员工号 |
1 |
2 |
3 |
4 |
|
| 甲组 |
件数 |
9 |
11 |
1l |
9 |
| 员工号 |
1 |
2 |
3 |
4 |
|
| 乙组 |
件数 |
9 |
8 |
10 |
9 |
(1)用茎叶图表示两组的生产情况;
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率.
(注:方差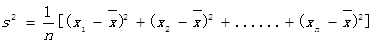 ,其中
,其中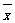 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)
已知向量 ,定义函数
,定义函数
(1)求函数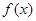 的表达式,并指出其最大最小值;
的表达式,并指出其最大最小值;
(2)在锐角 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且 求
求 的面积S。
的面积S。
设 为非负实数,满足
为非负实数,满足 ,证明:
,证明: .
.
函数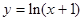
(1)若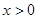 ,证明
,证明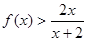 ;
;
(2)若不等式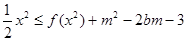 时
时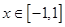 和
和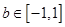 都恒成立,求实数
都恒成立,求实数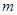 的取值范围。
的取值范围。
已知 ,对
,对 :
: 和
和 是方程
是方程 的两个根,不等式
的两个根,不等式 对任意实数
对任意实数 恒成立;
恒成立; :函数
:函数 有两个零点,求使“
有两个零点,求使“ 且
且 ”为真命题的实数的取值范围。
”为真命题的实数的取值范围。