已知向量 ,动点
,动点 到定直线
到定直线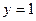 的距离等于
的距离等于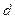 ,并且满足
,并且满足 ,其中
,其中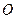 为坐标原点,
为坐标原点,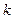 为非负实数.
为非负实数.
(1)求动点 的轨迹方程
的轨迹方程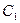 ;
;
(2)若将曲线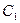 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(3)若(2)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足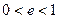 ,当
,当 是曲线
是曲线 的两个焦点时,则圆锥曲线上恒存在点
的两个焦点时,则圆锥曲线上恒存在点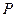 ,使得
,使得 成立,求实数
成立,求实数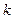 的取值范围.
的取值范围.
(本小题满分12分)已知关于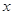 的函数
的函数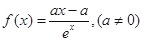
(1)当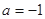 时,求函数
时,求函数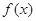 的极值;
的极值;
(2)若函数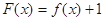 没有零点,求实数
没有零点,求实数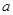 的取值范围.
的取值范围.
(本小题满分12分)设函数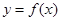 在
在 上的导函数为
上的导函数为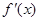 ,
,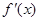 在
在 上的导函数为
上的导函数为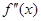 ,若在
,若在 上,
上,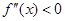 恒成立,则称函数
恒成立,则称函数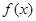 在
在 上为“凸函数”.已知
上为“凸函数”.已知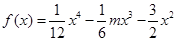 .
.
(1)若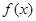 为区间
为区间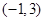 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数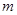 的值;
的值;
(2)若当实数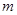 满足
满足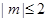 时,函数
时,函数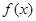 在
在 上总为“凸函数”,求
上总为“凸函数”,求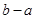 的最大值.
的最大值.
(本小题满分10分)已知函数
(1)若直线 与曲线
与曲线 相切,求实数
相切,求实数 的值;
的值;
(2)若 ,比较
,比较 与
与 的大小
的大小
(本小题满分12分)在锐角 中,已知内角
中,已知内角 、
、 、
、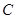 所对的边分别为
所对的边分别为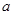 、
、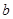 、
、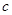 ,向量
,向量 ,且向量
,且向量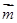 ,
, 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 的面积
的面积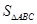 的最大值.
的最大值.
(本小题满分12分)已知函数 ,
,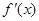 是
是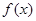 的导函数.
的导函数.
(1)求函数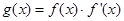 的最小值及相应的
的最小值及相应的 值的集合;
值的集合;
(2)若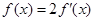 ,求
,求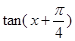 的值.
的值.