点 是单位圆上的两点,
是单位圆上的两点, 点分别在第一、二象限,点
点分别在第一、二象限,点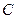 是圆与
是圆与 轴正半轴的交点,
轴正半轴的交点, 是正三角形,若点
是正三角形,若点 的坐标为
的坐标为 ,记
,记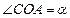 .
.
(1)求 的值; (2)求
的值; (2)求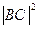 的值.
的值.
(本小题满分14分)如图,某城市有一条公路从正西方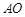 通过市中心
通过市中心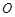 后转向东偏北
后转向东偏北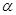 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心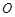 的距离
的距离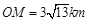 ,且
,且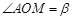 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站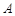 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在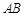 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中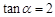 ,
,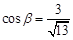 ,
,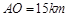 .
.
(1)求大学 与站
与站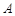 的距离
的距离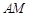 ;
;
(2)求铁路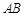 段的长
段的长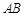 .
.
(本小题满分14分)如图,四棱锥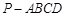 中,底面
中,底面 为矩形,
为矩形,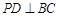 ,
,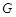 为
为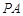 上一点.
上一点.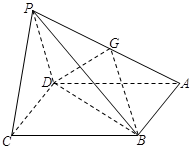
(1)求证:平面
 平面
平面 ;
;
(2)若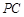 ∥平面
∥平面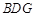 ,求证:
,求证: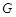 为
为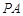 的中点.
的中点.
(本小题满分14分)在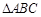 中,
中,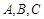 的对边分别为
的对边分别为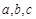 ,且
,且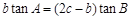 .
.
(1)求角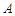 的大小;
的大小;
(2)设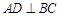 ,
,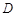 为垂足,若
为垂足,若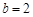 ,
,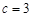 ,求
,求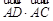 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
(1)已知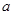 ,
,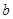 都是正数,且
都是正数,且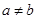 ,求证:
,求证: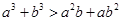 ;
;
(2)已知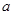 ,
,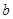 ,
,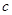 都是正数,求证:
都是正数,求证: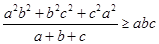 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆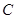 的参数方程为
的参数方程为 (
(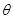 为参数).
为参数).
(1)以原点为极点、 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆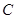 的极坐标方程;
的极坐标方程;
(2)已知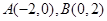 ,圆
,圆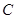 上任意一点
上任意一点 ,求
,求 面积的最大值.
面积的最大值.