(本小题满分14分)如图,某城市有一条公路从正西方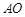 通过市中心
通过市中心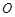 后转向东偏北
后转向东偏北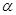 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心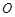 的距离
的距离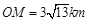 ,且
,且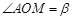 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站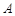 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在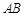 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中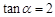 ,
,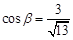 ,
,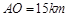 .
.
(1)求大学 与站
与站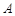 的距离
的距离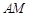 ;
;
(2)求铁路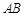 段的长
段的长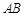 .
.
已知函数f(x)=ax+ln x,其中a为常数,e为自然对数的底数.
(1)当a=-1时,求f(x)的最大值;
(2)当a=-1时,试推断方程|f(x)|=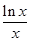 +
+ 是否有实数解,并说明理由.
是否有实数解,并说明理由.
已知Sn是等比数列{an}的前n项和,S4,S2,S3成等差数列,且a2+a3+a4=-18.
(1)求数列{an}的通项公式;
(2)是否存在正整数n,使得Sn≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
已知椭圆C: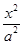 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,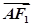 ·
· =0,3|
=0,3| |·|
|·|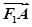 |=-5
|=-5 ·
·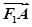 ,|
,| |=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
|=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
(1)求椭圆C的方程;
(2)线段OF2(O为坐标原点)上是否存在点M(m,0),使得 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.