已知函数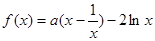 ,
,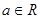 .
.
(1)若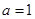 ,判断函数
,判断函数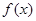 是否存在极值,若存在,求出极值;若不存在,说明理由;
是否存在极值,若存在,求出极值;若不存在,说明理由;
(2)设函数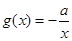 ,若至少存在一个
,若至少存在一个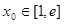 ,使得
,使得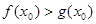 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(3)求函数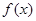 的单调区间.
的单调区间.
已知椭圆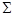 :
: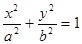 (
(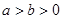 )的上顶点为
)的上顶点为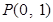 ,过
,过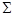 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为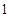 .若有一个菱形
.若有一个菱形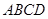 的顶点
的顶点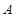 、
、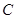 在椭圆
在椭圆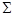 上,该菱形对角线
上,该菱形对角线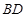 所在直线的斜率为
所在直线的斜率为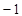 .
.
(1)求椭圆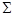 的方程;
的方程;
(2)当直线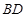 过点
过点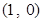 时,求直线
时,求直线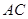 的方程;
的方程;
(3)当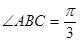 时,求菱形
时,求菱形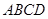 面积的最大值.
面积的最大值.
各项均不相等的等差数列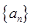 的前四项的和为
的前四项的和为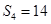 ,且
,且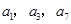 成等比数列.
成等比数列.
(1)求数列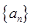 的通项公式
的通项公式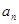 与前n项和
与前n项和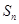 ;
;
(2)记 为数列
为数列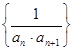 的前n项和,若
的前n项和,若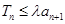 对任意的正整数n都成立,求实数λ的最小值.
对任意的正整数n都成立,求实数λ的最小值.
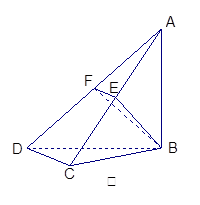
如图甲,在平面四边形ABCD中,已知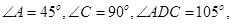
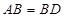 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD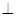 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(1)求证:DC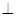 平面ABC;
平面ABC;
(2)设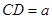 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.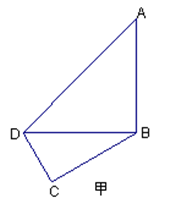
某中学高三年级从甲(文)、乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.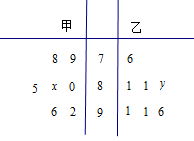
(1)求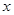 和
和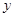 的值;
的值;
(2)计算甲组7位学生成绩的方差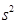 ;
;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.