如下图，已知点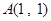
和单位圆上半部分上的动点
．
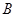（1）若
，求向量
；
（2）求
的最大值．
在
中，
分别为角
的对边，的面积
满足
.
（Ⅰ）求角A的值；
（Ⅱ）若
，设角B的大小为x,用x表示c并求的取值范围.
设数列
的各项均为正数，其前n项的和为
，对于任意正整数m,n, 
恒成立.
(Ⅰ)若
=1,求
及数列的通项公式;
(Ⅱ)若
,求证:数列是等比数列.
设函数
；
(Ⅰ)求证：函数
在
上单调递增；
(Ⅱ)设
，若直线PQ∥x轴，求P,Q两点间的最短距离.
如图，已知椭圆E的中心是原点O，其右焦点为F(2，0)，过x轴上一点A(3,0)作直线
与椭圆E相交于P,Q两点,且
的最大值为
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设
,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线，若共线请证明；反之说明理由.
如图，四边形PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
.
(Ⅰ)若M为PA中点,求证:AC∥平面MDE;
(Ⅱ)求平面PAD与PBC所成锐二面角的大小.