设数列 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为 ,对于任意正整数m,n,
,对于任意正整数m,n,  恒成立.
恒成立.
(Ⅰ)若 =1,求
=1,求 及数列
及数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求证:数列
,求证:数列 是等比数列.
是等比数列.
已知角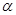 的终边在
的终边在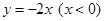 上,求
上,求
(1)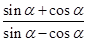 的值;
的值;
(2) 的值.
的值.
已知函数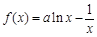 ,
,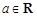 .
.
(1)若曲线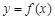 在点
在点 处的切线与直线
处的切线与直线 垂直,求
垂直,求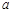 的值;
的值;
(2)求函数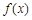 的单调区间;(3)当
的单调区间;(3)当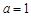 ,且
,且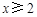 时,证明:
时,证明: .
.
已知抛物线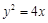 ,点
,点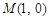 关于
关于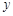 轴的对称点为
轴的对称点为 ,直线
,直线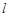 过点
过点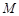 交抛物线于
交抛物线于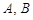 两点.
两点.
(1)证明:直线 的斜率互为相反数;
的斜率互为相反数;
(2)求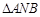 面积的最小值;
面积的最小值;
(3)当点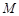 的坐标为
的坐标为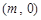 ,
, 且
且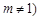 .根据(1)(2)推测并回答下列问题(不必说明理由):
.根据(1)(2)推测并回答下列问题(不必说明理由):
①直线 的斜率是否互为相反数? ②
的斜率是否互为相反数? ②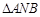 面积的最小值是多少?
面积的最小值是多少?
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮.现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是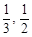 .两人投篮3次,且第一次由甲开始投篮,假设每人每次投篮命中与否均互不影响.
.两人投篮3次,且第一次由甲开始投篮,假设每人每次投篮命中与否均互不影响.
(1)求3次投篮的人依次是甲、甲、乙的概率;
(2)若投篮命中一次得1分,否则得0分,用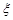 表示甲的总得分,求
表示甲的总得分,求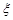 的分布列和数学期望.
的分布列和数学期望.
如图所示,在边长为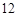 的正方形
的正方形 中,点
中,点 在线段
在线段 上,且
上,且 ,
, ,作
,作

 ,分别交
,分别交
 ,
, 于点
于点 ,
,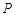 ,作
,作

 ,分别交
,分别交 ,
, 于点
于点 ,
,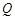 ,将该正方形沿
,将该正方形沿 ,
, 折叠,使得
折叠,使得 与
与 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱 .
.
(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积;
的体积;
(3)求平面 与平面
与平面 所成角的余弦值.
所成角的余弦值.