(本小题满分13分)
正数数列{an}的前n项和为Sn,且2.
(1)试求数列{an}的通项公式;
(2)设bn=,{bn}的前n项和为Tn,求证:Tn<.
(本小题满分13分)
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC= AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
(本小题满分13分)
已知 ,
,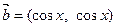 ,f(x)=
,f(x)=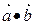

⑴ 求f(x)的最小正周期和单调增区间;
⑵ 如果三角形ABC中,满足f(A)=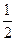 ,求角A的值.
,求角A的值.
(本小题满分13分)
已知函数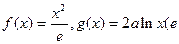 为自然对数的底数)
为自然对数的底数)
(1)求 的单调区间,若
的单调区间,若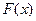 有最值,请求出最值;
有最值,请求出最值;
(2)是否存在正常数 ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出 的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线, 交E于A,B两点,
交E于A,B两点,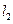 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求 k的取值范围;
k的取值范围;
(3)求 的取值范围。
的取值范围。
(本小题满分13分)
在数列 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列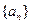 的通项公式
的通项公式 ;
;
(2)设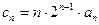 ,求数列
,求数列 的前
的前 项和。
项和。