选修4—4:坐标系与参数方程
在平面直角坐标系中,直线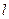 过点
过点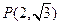 且倾斜角为
且倾斜角为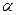 ,以坐标原点为极点,
,以坐标原点为极点,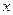 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线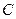 的极坐标方程为
的极坐标方程为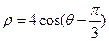 ,直线
,直线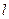 与曲线
与曲线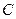 相交于
相交于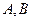 两点;
两点;
(1)若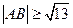 ,求直线
,求直线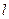 的倾斜角
的倾斜角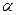 的取值范围;
的取值范围;
(2)求弦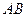 最短时直线
最短时直线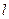 的参数方程。
的参数方程。
(选修4—2:矩阵与变换)
若矩阵 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为 ,求矩阵
,求矩阵 的逆矩阵
的逆矩阵 .
.
(选修4—1:几何证明选讲)
在 中,已知
中,已知 是
是 的平分线,
的平分线, 的外接圆交
的外接圆交 于点
于点 .若
.若 ,
, ,求
,求 的长.
的长.
(本小题满分16分)设函数 (其中
(其中 ),且存在无穷数列
),且存在无穷数列 ,使得函数在其定义域内还可以表示为
,使得函数在其定义域内还可以表示为 .
.
(1)求 (用
(用 表示);
表示);
(2)当 时,令
时,令 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若数列 是公差不为零的等差数列,求
是公差不为零的等差数列,求 的通项公式.
的通项公式.
(本小题满分16分)设函数 ,
, .
.
(1)当 时,函数
时,函数 与
与 在
在 处的切线互相垂直,求
处的切线互相垂直,求 的值;
的值;
(2)若函数 在定义域内不单调,求
在定义域内不单调,求 的取值范围;
的取值范围;
(3)是否存在实数 ,使得
,使得 对任意正实数
对任意正实数 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分16分)如图,在平面直角坐标系 中,椭圆
中,椭圆 的离心率为
的离心率为 ,直线
,直线 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于
交于 、
、 两点.当直线
两点.当直线 垂直于
垂直于 轴且点
轴且点 为椭圆
为椭圆 的右焦点时, 弦
的右焦点时, 弦 的长为
的长为 .
.
(1)求椭圆 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,点
,点 在第一象限且横坐标为
在第一象限且横坐标为 ,连结点
,连结点 与原点
与原点 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,求
,求 的面积;
的面积;
(3)是否存在点 ,使得
,使得 为定值?若存在,请指出点
为定值?若存在,请指出点 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.