三棱锥P—ABC中,△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥平面ABC,D、E分别为AB、PB的中点.
(1)求证:AC⊥PD;
(2)求二面角E—AC—B的正切值;
|
(3)求三棱锥P—CDE与三棱锥P—ABC的体积之比.
(本小题满分12分)已知函数 .
.
(1)若函数 ,求函数
,求函数 的单调区间;
的单调区间;
(2)设直线 为函数
为函数 的图像上点
的图像上点 处的切线,证明:在区间
处的切线,证明:在区间 上存在唯一
上存在唯一 ,直线
,直线 与曲线
与曲线 相切.
相切.
(本小题满分12分)若函数 的图象与直线
的图象与直线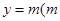 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为 .
.
(1)求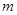 的值;
的值;
(2)若点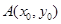 是
是 图象的对称中心,且
图象的对称中心,且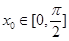 ,求点A的坐标.
,求点A的坐标.
(本小题满分12分)已知函数 .
.
(1)求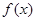 的单调区间;
的单调区间;
(2)设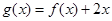 ,若
,若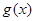 在
在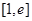 上不单调且仅在
上不单调且仅在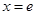 处取得最大值,求
处取得最大值,求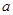 的取值范围.
的取值范围.
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,
, ,
, 为锐角,且
为锐角,且 ,求
,求 面积
面积 的最大值.
的最大值.
设命题 在区间
在区间 上是减函数;命题
上是减函数;命题
 是方程
是方程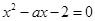 的两个实根,且不等式
的两个实根,且不等式 对任意的实数
对任意的实数 恒成立,若
恒成立,若 为真,试求实数
为真,试求实数 的取值范围.
的取值范围.