已知函数 ,
,
(1)若对任意的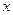 有
有 成立,求
成立,求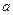 的取值范围;
的取值范围;
(2)若不等式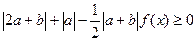 ,对于任意的
,对于任意的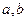 都成立,求
都成立,求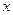 的取值范围。
的取值范围。
已知曲线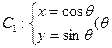 为参数),曲线
为参数),曲线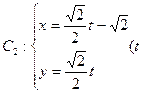 为参数)。
为参数)。
(1)指出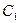 和
和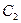 各是什么曲线,并说明
各是什么曲线,并说明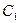 和
和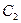 公共点的个数;
公共点的个数;
(2)若把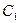 ,
,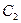 上各点的纵坐标都压缩为原来的一半,分别得到曲线
上各点的纵坐标都压缩为原来的一半,分别得到曲线 、
、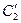 ,写出
,写出 ,
,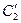 的参数方程。
的参数方程。 与
与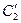 的公共点的个数和
的公共点的个数和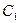 与
与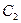 公共点的个数是否相同?说明你的理由。
公共点的个数是否相同?说明你的理由。
已知直线的极坐标方程为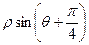 =
=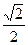 ,圆M的参数方程为
,圆M的参数方程为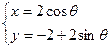 (其中
(其中 为参数)。
为参数)。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值。
已知直线 的参数方程为
的参数方程为 为参数),直线
为参数),直线 与曲线
与曲线 为参数)相交于两点A、B,求点P(1,1)到A、B两点的距离之积。
为参数)相交于两点A、B,求点P(1,1)到A、B两点的距离之积。
(本小题满分14分)
已知数列 的前n项和为
的前n项和为 ,且
,且 ,
,
(1)试计算 ,并猜想
,并猜想 的表达式;
的表达式;
(2) 证明你的猜想,并求出 的表达式。
的表达式。