(本小题满分12分)已知函数 .
.
(1)求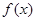 的单调区间;
的单调区间;
(2)设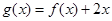 ,若
,若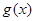 在
在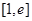 上不单调且仅在
上不单调且仅在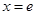 处取得最大值,求
处取得最大值,求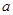 的取值范围.
的取值范围.
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且
(Ⅰ)写出年利润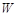 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大
已知直角梯形 ,
, 是
是 边上的中点(如图甲),
边上的中点(如图甲), ,
, ,
,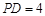 ,将
,将 沿
沿 折到
折到 的位置,使
的位置,使 ,点
,点 在
在 上,且
上,且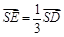 (如图乙)
(如图乙)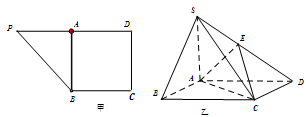
(Ⅰ)求证: 平面ABCD.
平面ABCD.
(Ⅱ)求二面角E−AC−D的余弦值
某旅游公司提供甲、乙、丙三处旅游景点,游客选择游玩哪个景点互不影响,已知某游客选择游甲地而不选择游乙地和丙地的概率为0.08,选择游甲地和乙地而不选择游丙地的概率为0.12,在甲、乙、丙三处旅游景点中至少选择游一个景点0.88,用 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
(Ⅰ)记“函数 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求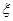 的概率分布列及数学期望.
的概率分布列及数学期望.
已知函数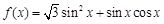 .
.
(Ⅰ)求函数 在区间
在区间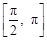 上的零点;
上的零点;
(Ⅱ)设 ,求函数
,求函数 的图象的对称轴方程
的图象的对称轴方程
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为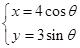 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线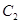 的极坐标方程为
的极坐标方程为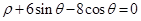 (
( )
)
(Ⅰ)求曲线 的普通方程和曲线
的普通方程和曲线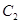 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线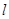 :
: 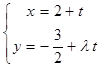 (
( 为参数)过曲线
为参数)过曲线 与
与 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线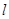 平行且与曲线
平行且与曲线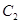 相切的直线方程
相切的直线方程