对于函数 ,若在定义域内存在实数
,若在定义域内存在实数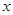 ,满足
,满足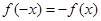 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(Ⅰ)已知二次函数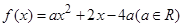 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(Ⅱ)若 是定义在区间
是定义在区间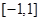 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(Ⅲ)若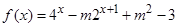 为定义域
为定义域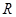 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
已知命题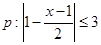 ;
;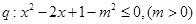 若
若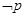 是
是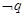 的充分非必要条件,试求实数
的充分非必要条件,试求实数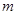 的取值范围.
的取值范围.
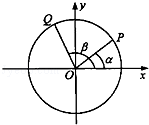
如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(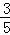 ,
,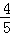 ).
).
(1)求sin2α的值;
(2)若β﹣α=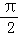 ,求cos(α+β)的值.
,求cos(α+β)的值.
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为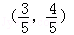 ,点B在第二象限,且△AOB为正三角形.
,点B在第二象限,且△AOB为正三角形.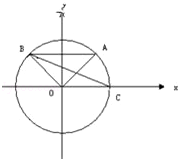
(Ⅰ)求sin∠COA;
(Ⅱ)求△BOC的面积.
已知点A(2,0),B(0,2),点C(x,y)在单位圆上.
(1)若|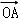 +
+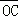 |=
|=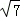 (O为坐标原点),求
(O为坐标原点),求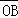 与
与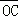 的夹角;
的夹角;
(2)若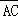 ⊥
⊥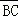 ,求点C的坐标.
,求点C的坐标.
已知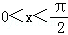 ,用单位圆求证下面的不等式:
,用单位圆求证下面的不等式:
(1)sinx<x<tanx;
(2)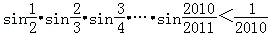 .
.