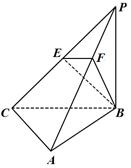
如图,三棱锥 中,
中,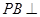 底面
底面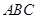 ,
, ,
, ,
, 为
为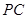 的中点,点
的中点,点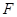 在
在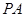 上,且
上,且 .
.
(Ⅰ)求证:平面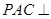 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面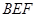 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
(本小题满分12分)
设f(x)是定义在[-1,1]上的奇函数,对于任意的
 当
当 时,都
时,都
有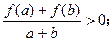
(1)若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集,求c的取值范围;
(2)判断函数f(x)在[-1,1]上的单调性,并用定义证明。
(本小题满分12分)
已知p: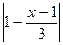 ≤2, q:
≤2, q: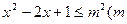 >0)
>0)
若非p是非q的必要不充分条件,求实数m的取值范围。
(本小题满分10 分)
解关于x的不等式: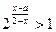 (
(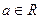 )。
)。
函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线3x+y+2=0.
(1)求a,b的值; (2)求函数的极大值与极小值的差.
已知函数
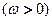 的最小正周期为
的最小正周期为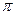
(1)求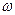 的值;(2)求函数f(x)的单调递增区间;
的值;(2)求函数f(x)的单调递增区间;
(3)求函数f(x)在区间[0,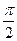 ]上的取值范围.
]上的取值范围.