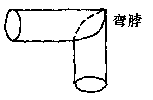
如图，铁匠师傅在打制烟筒弯脖时，为确保对接成直角，在铁板上的下剪线正好是余弦曲线：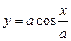
的一个周期的图象，问弯脖的直径为12 
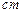时，
应是多少?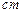
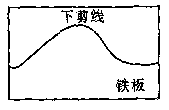
如图所示的多面体，它的正视图为直角三角形，侧视图为正三角形，俯视图为正方形（尺寸如图所示），E为VB的中点．
(1)求证：VD∥平面EAC；
(2)求二面角A—VB—D的余弦值．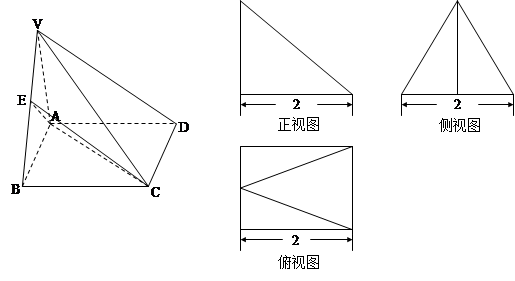
一个盒子装有6张卡片，上面分别写着如下6个定义域为R的函数：
，
，
，
，
，
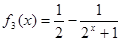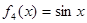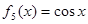(1)现从盒子中任取两张卡片，将卡片上的函数相加得到一个新函数，求所得函数是奇函数的概率；
(2)现从盒子中逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望．
在△ABC中，A、B、C的对边分别为a、b、c，向量
，
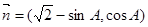，若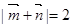
．
(1)求角A的大小；
(2)若
，且
，求△ABC的面积
已知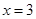
是函数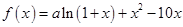
的一个极值点。
（1）求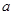
；
（2）求函数
的单调区间；
（3）若直线
与函数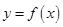
的图象有3个交点，求
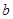的取值范围
知函数
的图象在点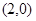
处的切线方程是
.
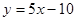（1）求函数
的解析式；
（2）设函数
，若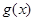
的极值存在，求实数
的取值范围