2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断。5月12日晚,抗震救灾指挥部决定从水路(一支队伍)、陆路(东南和西北两个方向各一支队伍)和空中(一支队伍)同时向灾区挺进。在5月13日,仍时有较强余震发生,天气状况也不利于空中航行。已知当天从水路抵达灾区的概率是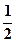 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是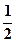 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是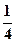 。(1)求在5月13日恰有1支队伍抵达灾区的概率;(2)求在5月13日抵达灾区的队伍数
。(1)求在5月13日恰有1支队伍抵达灾区的概率;(2)求在5月13日抵达灾区的队伍数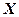 的数学期望。
的数学期望。
已知定圆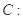
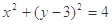 ,定直线
,定直线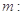
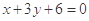 ,过
,过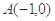 的一条动直线
的一条动直线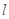 与直线相
与直线相
交于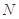 ,与圆
,与圆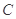 相交于
相交于 两点,
两点,
(1)当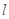 与
与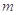 垂直时,求出
垂直时,求出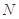 点的坐标,并证明:
点的坐标,并证明: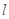 过圆心
过圆心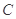 ;
;
(2)当 时,求直线
时,求直线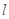 的方程;
的方程;
已知函数  .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)在 中,内角
中,内角 所对边分别为
所对边分别为 ,
, ,若对任意的
,若对任意的 不等式
不等式 恒
恒
成立,求 面积的最大值.
面积的最大值.
(本小题满分13分)已知直线 ,
, 相交于点
相交于点 .
.
(1)求点 的坐标;
的坐标;
(2)求以点 为圆心,且与直线
为圆心,且与直线 相切的圆的方程;
相切的圆的方程;
(3)若直线 与(2)中的圆
与(2)中的圆 交于
交于 、
、 两点,求
两点,求 面积的最大值及实数
面积的最大值及实数 的值.
的值.
(本小题满分13分)如图,在棱长均为 的直三棱柱
的直三棱柱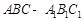 中,
中, 是
是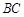 的中点.
的中点.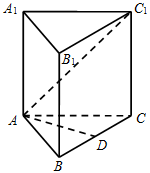
(1)求证: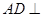 平面
平面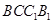 ;
;
(2)求直线 与面
与面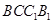 所成角的正弦值.
所成角的正弦值.
(本小题满分13分)在等比数列 中,已知
中,已知 ,
, ,
,
(1)求 的通项公式;
的通项公式;
(2)令 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.