(本小题满分13分)如图,在棱长均为 的直三棱柱
的直三棱柱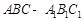 中,
中, 是
是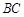 的中点.
的中点.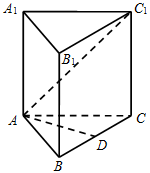
(1)求证: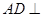 平面
平面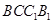 ;
;
(2)求直线 与面
与面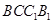 所成角的正弦值.
所成角的正弦值.
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α=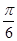 ,圆C的极坐标方程为
,圆C的极坐标方程为 =
= cos(θ-
cos(θ- ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,AD、CE的延长线交于点B,且AD=DE,AB=2AC.
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(本小题满分12分)已知函数f(x)=x+alnx在x=1处的切线l与直线x+2y=0垂直,函数g(x)=f(x)+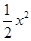 -bx.
-bx.
(Ⅰ)求实数a的值;
(Ⅱ)设x1,x2 (x1<x2)是函数g(x)的两个极值点,若b≥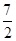 ,求g(x1)-g(x2)的最小值.
,求g(x1)-g(x2)的最小值.
(本小题满分12分)已知直线l的方程为y=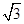 x-2
x-2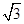 ,又直线l过椭圆C:
,又直线l过椭圆C: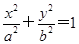 (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为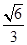 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设 =λ
=λ (0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.