设集合A={a,b},集合B={a+1,5},若A∩B={2},求A并写出集合A的所有子集.
在△ABC中,角A,B,C所对的边分别为a,b,c,且1+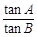 =
=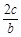 .
.
(Ⅰ)求角A;
(Ⅱ)已知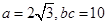 ,求
,求 的值。
的值。
如图,设F(-c,0)是椭圆 的左焦点,直线l:x=-
的左焦点,直线l:x=-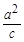 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。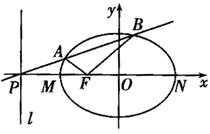
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P的直线m与椭圆相交于不同的两点A,B。
①证明:∠AFM=∠BFN;
②求△ABF面积的最大值。
如图,已知平行六面体ABCD—A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O。
(Ⅰ)求证:平面O1DC⊥平面ABCD;
(Ⅱ)若∠A1AB=60°,求平面BAA1与平面CAA1的夹角的余弦值。
已知函数 (
(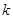 为常数,
为常数, 且
且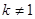 ),且数列
),且数列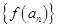 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
(Ⅰ)求证:数列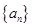 是等比数列;
是等比数列;
(Ⅱ)若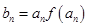 ,当
,当 时,求数列
时,求数列 的前n项和
的前n项和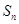 。
。
某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。
(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。