已知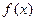 是定义在
是定义在 ,
,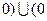 ,
,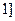 上的奇函数,当
上的奇函数,当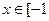 ,
,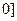 时,
时,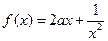 (a为实数).
(a为实数).
(1)当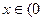 ,
,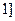 时,求
时,求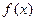 的解析式;
的解析式;
(2)若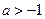 ,试判断
,试判断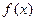 在[0,1]上的单调性,并证明你的结论;
在[0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当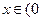 ,
,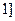 时,
时,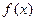 有最大值
有最大值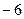 .
.
在某海滨城市附近海面有一台风,据测,当前台风中心位于城市O(如图)的东偏南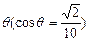 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?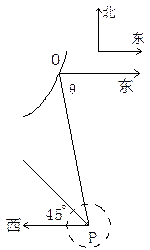
设 数列
数列 满足:
满足:
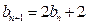 ,
,
(1)求证:数列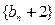 是等比数列(要指出首项与公比),
是等比数列(要指出首项与公比),
(2)求数列 的通项公式.
的通项公式.
在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足:2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积。
有三面不同的旗帜,取一面或多面纵列为信号,当三面全部挂出时,红色的必须悬挂在最上端,共能组成多少种信号?
将8辆不通汽车停放在12个车库中,要求剩余的车库必须相邻在一起,共有多少种放法?