已知函数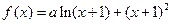 在
在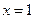 处有极值.
处有极值.
(Ⅰ)求实数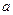 值;
值;
(Ⅱ)求函数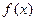 的单调区间;
的单调区间;
(Ⅲ)令 ,若曲线
,若曲线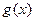 在
在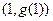 处的切线与两坐标轴分别交于
处的切线与两坐标轴分别交于 ,
,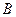 两点(
两点( 为坐标原点),求
为坐标原点),求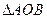 的面积.
的面积.
下面是一周内某地申领结婚证的新郎与新娘的年龄,记作(新郎年龄y,新娘年龄x):
(37,30),(30,27),(65,56),(45,40),(32,30),(28,26),(45,31),(29,24),(26,23),(28,25),(42,29),(36,33),(32,29),(24,22),(32,33),(ZI,29),(37,46),(28,25),(33,34),(21,23),(24,23),(49,44),(28,29),(30,30),(24,25),(22,23),(68,60),(25,25),(32,27),(42,37),(24,24),(24,22),(28,27),(36,31),(23,24),(30,26)
以下考虑y关于x的回归问题:
(1)如果每个新郎和新娘都同岁,穿过这些点的回归直线的斜率和截距等于什么?
(2)如果每个新郎比他的新娘大5岁,穿过这些点的回归直线的斜率和截距等于什么?
(3)如果每个新郎比他的新娘大10%,穿过这些点的回归直线的斜率和截距等于什么?
(4)对于上面的实际年龄作出回归直线;
(5)从这条回归直线,你对新娘和新郎的年龄模型可得出什么结论?
为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如下数据:
| 广告费用(千元) |
1.0 |
4.0 |
6.0 |
10.0 |
14.0 |
| 销售额(千元) |
19.0 |
44.0 |
40.0 |
52.0 |
53.0 |
(1)在同一张图上画散点图,直线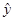 (1)=24+2.5x,
(1)=24+2.5x,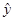 (2)=
(2)=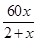 ;
;
(2)比较所画直线与曲线,哪一条更能表现这组数据之间的关系?
(3)分别计算用直线方程与曲线方程得到在5个x点处的销售额预测值、预测值与实际预测之间的误差,最后比较两个误差绝对值之和的大小。
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如图所示.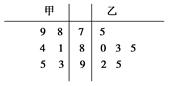
从平均成绩及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
| 分组 |
频数 |
频率 |
|
| 一组 |
0≤t<5 |
0 |
0 |
| 二组 |
5≤t<10 |
10 |
0.10 |
| 三组 |
10≤t<15 |
10 |
② |
| 四组 |
15≤t<20 |
① |
0.50 |
| 五组 |
20≤t≤25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
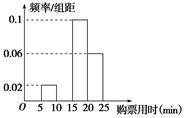
解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: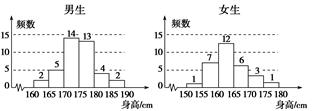
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185 cm之间的概率.