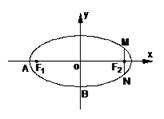
如图，在直角坐标系
中，已知椭圆
的离心率e＝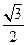
，左右两个焦分别为
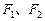．过右焦点
且与
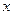轴垂直的
直线与椭圆
相交M、N两点，且|MN|=1．
(Ⅰ) 求椭圆的方程；
(Ⅱ) 设椭圆的左顶点为A,下顶点为B，动点P满足
，
（
）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆上.
（本小题满分12分）已知集合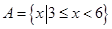
，
．
（1）分别求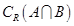
，
；
（2）已知
，若
，求实数
的取值集合
（本小题满分12分）设集合A＝{x2 , 2x-1, -4} ，B＝{x-5, 1-x,9}. 若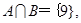
求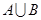
.
已知数列
的首项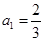
，
，
…．
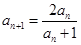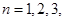（1）证明：数列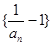
是等比数列；
（2）数列
的前
项和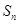
．
某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（1）求第n年初M的价值
的表达式；
（2）设
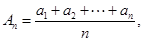若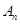
大于80万元，则M继续使用，否则须在第n年初对M更新，
证明：第6年初仍可对M继续使用．
已知数列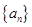
前
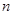项和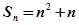
（1）求数列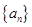的通项公式；
（2）令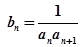
，求证：数列{
}的前n项和
.