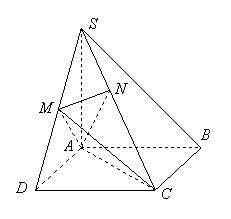
如图,在四棱锥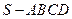 中,底面
中,底面 是正方形,
是正方形,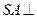 底面
底面 ,
,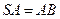 , 点
, 点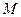 是
是 的中点,
的中点,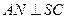 ,且交
,且交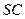 于点
于点 .
.
(I)求证: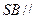 平面
平面 ;
;
(II)求二面角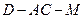 的余弦值大小;
的余弦值大小;
(III)求证:平面 ⊥平面
⊥平面 .
.
定义符号函数sgnx=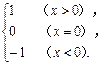 当x∈R时,解不等式(x+2)>(2x-1)sgnx.
当x∈R时,解不等式(x+2)>(2x-1)sgnx.
一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,设该车从各站出发时邮政车内的邮袋数构成一个有穷数列 ,
,
试求:(1)
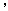
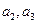
(2)邮政车从第k站出发时,车内共有邮袋数是多少个?
(3)求数列 的前k项和
的前k项和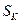 并证明:
并证明: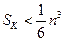
已知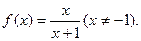
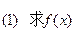 的单调区间;
的单调区间;
(2)若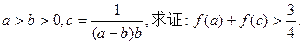
某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为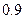 万元,年维修费用第一年是
万元,年维修费用第一年是 万元,以后逐年递增
万元,以后逐年递增 万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
已知函数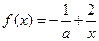 ,若
,若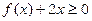 在(0,+
在(0,+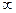 )上恒成立,求
)上恒成立,求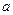 的取值范围。
的取值范围。