已知数列 满足:
满足: 且对任意的
且对任意的 有
有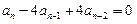 .
.
(Ⅰ)求数列 的通项公式
的通项公式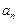 ;
;
(Ⅱ)是否存在等差数列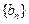 ,使得对任意的
,使得对任意的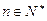 有
有 成立?证明你的结论
成立?证明你的结论
(本小题满分12分)已知定义域为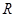 的函数
的函数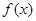 满足
满足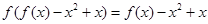
(1)若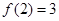 ,求
,求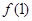 ;又若
;又若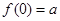 ,求
,求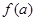 ;
;
(2)设有且仅有一个实数 ,使得
,使得 ,求函数
,求函数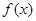 的解析式.
的解析式.
(本小题满分12分)已知函数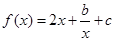 ,其中
,其中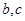 为常数且满足
为常数且满足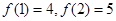 .
.
(1)求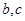 的值;
的值;
(2)证明函数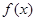 在区间
在区间 上是减函数,并判断
上是减函数,并判断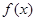 在
在 上的单调性;
上的单调性;
(3)若对任意的 ,总有
,总有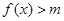 成立,求实数
成立,求实数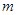 的取值范围.
的取值范围.
(本小题满分12分)《中华人民共和国个人所得税》规定,公民全月工资、薪金所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
| 全月应纳税所得额 |
税率(%) |
| 不超过500元的部分 |
5 |
| 超过500元至2000元的部分 |
10 |
| 超过2000元至5000元的部分 |
15 |
(1)设当月应激纳此项税款为 元,当月工资、薪金所得为
元,当月工资、薪金所得为 元,把
元,把 表示成
表示成 的函数;
的函数;
(2)某人一月份应激纳此项税款为26.78元,那么他当月的工资、薪金所得是多少?
(本小题满分12分)已知非空数集 ,且
,且 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当 变化时,若集合
变化时,若集合 中
中 的最小值为
的最小值为 ,求
,求 的值域.
的值域.
(本小题满分12分)已知二次函数 ,当
,当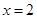 时函数取最小值-1,且
时函数取最小值-1,且
(1)求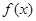 的解析式;
的解析式;
(2)若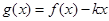 在区间
在区间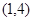 上不单调,求实数
上不单调,求实数 的取值范围.
的取值范围.