某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是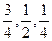 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |
 组 组 |
 组 组 |
 组 组 |
| 疫苗有效 |
673 |
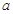 |
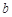 |
| 疫苗无效 |
77 |
90 |
 |
已知在全体样本中随机抽取1个,抽到 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在 组抽取样本多少个?
组抽取样本多少个?
(2)已知 ,
, ,求通过测试的概率.
,求通过测试的概率.
已知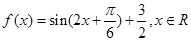 .
.
(1)求函数 的最小正周期和单调增区间.
的最小正周期和单调增区间.
(2)函数 的图象可以由函数
的图象可以由函数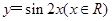 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
已知 ,求
,求 的值.
的值.
设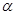 为第四象限角,其终边上的一个点是
为第四象限角,其终边上的一个点是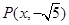 ,且
,且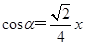 ,求
,求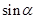 和
和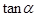 .
.
各项均为正数的数列 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有  .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和
项和 .
.