四棱锥P—ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°
某电脑公司有6名产品推销员,其中5名推销员的工作年限与年推销金额数据如下表:
| 推销员编号 |
1 |
2 |
3 |
4 |
5 |
工作年限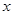 (年) (年) |
3 |
5 |
6 |
7 |
9 |
年推销金额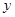 (万元) (万元) |
2 |
3 |
3 |
4 |
5 |
(1)求年推销金额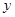 关于工作年限
关于工作年限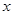 的线性回归方程.
的线性回归方程.
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
已知 是复数,
是复数,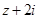 ,
,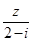 均为实数,且复数
均为实数,且复数 在复平面上对应的点在第四象限.
在复平面上对应的点在第四象限.
(1)求复数 (2)试求实数
(2)试求实数 的取值范围.
的取值范围.
如右图,设由抛物线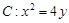 与过它的焦点F的直线
与过它的焦点F的直线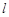 所围成封闭曲面图形的面积为
所围成封闭曲面图形的面积为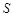 (阴影部分)。
(阴影部分)。
(1)设直线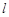 与抛物线
与抛物线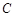 交于两点
交于两点 ,且
,且 ,直线
,直线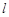 的斜率为
的斜率为 ,试用
,试用 表示
表示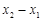 ;
;
(2)求 的最小值。
的最小值。
已知函数 ,求导函数
,求导函数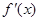 ,并确定
,并确定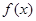 的单调区间
的单调区间
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度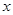 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?