如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明PA//平面BDE;
(2)求二面角B—DE—C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论. 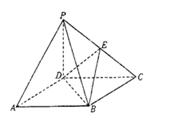
已知向量 ,其中
,其中 .
.
(1)试判断向量 与
与 能否平行,并说明理由?
能否平行,并说明理由?
(2)求函数 的最小值.
的最小值.
(本小题满分12分)
已知 ,数列
,数列 满足
满足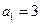 ,
, ,数列
,数列 满足
满足 ,
,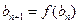 .
.
(1)求证:数列 为等比数列.
为等比数列.
(2)令 ,求证:
,求证: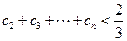 ;
;
(3)求证:
(本小题满分12分)
已知在平面直角坐标系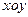 中,向量
中,向量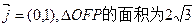 ,且
,且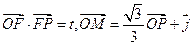 .
.
(I)设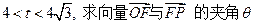 的取值范围;
的取值范围;
(II)设以原点O为中心,对称轴在坐标轴上,以F为右焦点的椭圆经过点M,且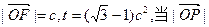 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
(本小题满分12分)
已知函数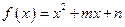 的图像过点
的图像过点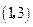 ,且
,且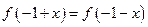 对任意实数都成
对任意实数都成
立,函数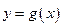 与
与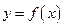 的图像关于原点对称.
的图像关于原点对称. 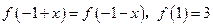 .
.
(Ⅰ)求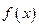 与
与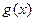 的解析式;
的解析式;
(Ⅱ)若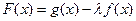 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围.
(本小题满分12分)
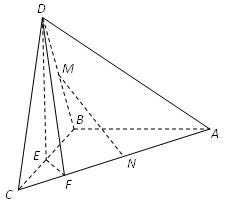
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.