已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在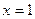 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(3)设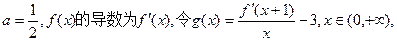
求证: .
.
已知函数f(x)=x3+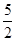 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+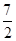 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为f’(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
在平面直角坐标系xoy中,已知椭圆C: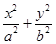 =1(a>b≥1)的离心率e=
=1(a>b≥1)的离心率e=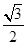 ,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
(1)求椭圆C的方程。
(2)设P为椭圆上一点,且满足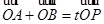 (O为坐标原点),当|AB|<
(O为坐标原点),当|AB|<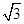 时,求实数t的取值范围.
时,求实数t的取值范围.
如图几何体中,四边形ABCD为矩形,AB=3BC=6,EF =4,BF=CF=AE=DE=2, EF∥AB,G为FC的中点,M为线段CD上的一点,且CM =2.
(1)证明:平面BGM⊥平面BFC;
(2)求三棱锥F-BMC的体积V.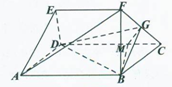
已知各项均为正数的等比数列{an}满足a3 =8,a5 +a7=160,{an}的前n项和为Sn.
(1)求an;
(2)若数列{bn}的通项公式为bn=(-1)n·n(n∈N+),求数列{an·bn}的前n项和Tn。
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
| A款手机 |
B款手机 |
C款手机 |
|
| 经济型 |
200 |
x |
y |
| 豪华型 |
150 |
160 |
z |
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(1)现用分层抽样的方法在A、B、C三款手机中抽取50部,求应在C款手机中抽取多少部?
(2)若y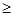 136,z
136,z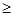 133,求C款手机中经济型比豪华型多的概率.
133,求C款手机中经济型比豪华型多的概率.