如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在 的上方,分别以△
的上方,分别以△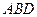 与△
与△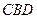 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离.
(本小题满分14分)
某慈善机构举办一次募捐演出,有一万人参加,每人一张门票,每张100元,在演出过程中穿插抽奖活动,第一轮抽奖从这一万张票根中随机抽取10张,其持有者获得价值1000元的奖品,并 参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数
参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 ,如果
,如果 则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
(I)已知小曹在第一轮抽奖中被抽中,求小曹在第二轮抽奖中获奖的概率;
(II)若小叶参加了此次活动,求小叶参加此次活动收益的期望;
(III)若此次募捐除奖品和奖金外,不计其它支出,该机构想获得96万元的慈善款,问该慈善机构此 次募捐是否能达到预期目标。
次募捐是否能达到预期目标。
(本小题满分12分)
某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
(I)若三辆汽车中恰有一辆汽车被堵的概率为 ,求走公路②堵的概率;
,求走公路②堵的概率;
(II)在(I)的条件下,求三辆汽车中恰有两辆汽车被堵的概率
(本小题满分12分)
用0,1,2,3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则这个数为凹数,
如524、746等都是凹数。那么这六个数字能组成多少个无重复数字凹数?
(本小题满分12分)
已知m, 的展开式中,x的系数为19。
的展开式中,x的系数为19。
求 的系数的最小值,并求此时
的系数的最小值,并求此时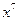 的系
的系 数。
数。
(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断休闲方式与性别是否有关。
(参考公式:
参考数据: )
)