(6分)已知函数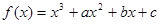 ,当
,当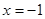 时,
时,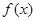 的极大值为7;当
的极大值为7;当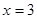 时,
时,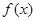 有极小值.求(1)
有极小值.求(1)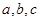 的值; (2)函数
的值; (2)函数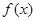 的极小值.
的极小值.
(本小题满分10分)一名学生在军训中练习射击项目,他射击一次,命中目标的概率是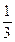 ,若连续射击6次,且各次射击是否命中目标相互之间没有影响.
,若连续射击6次,且各次射击是否命中目标相互之间没有影响.
(1)求这名学生在第3次射击时,首次命中目标的概率;
(2)求这名学生在射击过程中,恰好命中目标3次的概率.
(本小题满分14分) 对于函数f(x), 若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围
(本小题满分13分)某车间生产某机器的两种配件A和B,生产配件A成本费y 与该车间的工人人数x成反比,而成生产配件B成本费y
与该车间的工人人数x成反比,而成生产配件B成本费y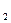 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这这两项费用y 和y
和y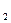 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少
(本小题满分12分)已知数列满足a 1=1,an+1=2an+1(n∈N*)
1=1,an+1=2an+1(n∈N*)
(1) 求证:数列 {an+1}是等比数列;
{an+1}是等比数列;
(2) 求{an}的通项公式.
(本小题满分12分)已知变量x,y满足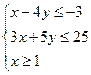 ,
,
1、求不等式组所表示图形的面积
2、求Z=2x+y的最大值和最小值.