如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积。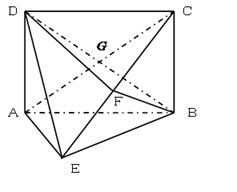
已知函数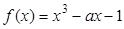 .
.
(Ⅰ)若 在实数集R上单调递增,求
在实数集R上单调递增,求 的范围;
的范围;
(Ⅱ)是否存在实数 使
使 在
在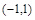 上单调递减.若存在求出
上单调递减.若存在求出 的范围,若不存在说明理由.
的范围,若不存在说明理由.
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈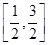 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为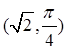 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 在直线上.
在直线上.
(1)求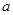 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;
(2)圆c的参数方程为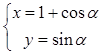 ,(
,(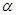 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.
在直角坐标系xOy中,直线l的参数方程为 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(1)求直线l与曲线C的平面直角坐标方程;
(2)设直线l与曲线C交于不同的两点A、B,若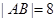 ,求α的值.
,求α的值.
为了降低能源损耗,某城市对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: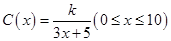 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.