（本小题满分14分）
直线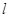
与椭圆
交于
，
两点，已知
，
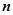
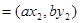，若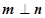
且椭圆的离心率
，又椭圆经过点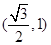
，
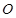为坐标原点.
（1）求椭圆的方程；
（2）若直线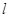过椭圆的焦点
（
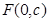为半焦距），求直线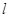的斜率
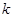的值；
（3）试问：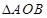
的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.
(1) 用辗转相除法求840与1 764的最大公约数.
(2)把“五进制”数
转化为“十进制”数，再把它转化为“八进制”数。
某市对一中学2010年高考语文和数学上线情况进行统计,随机抽查50名学生得到如下表格进行统计:统计人员甲计算数学
的观测值过程如下: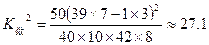
;类比甲的算法试计算语文的观测值是多少?(精确0.1)
（本小题满分10分）选修4-5：不等式选讲
已知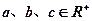
，且a+b+c=3，
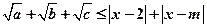对任意的
恒成立，求实数m的取值范围。
（本小题满分10分）选修4-4：坐标系于参数方程
在直角坐标系
中，以O为极点，x正半轴为极轴建立极坐标系，曲线
的极坐标方程为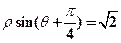
，M,N分别为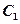与x轴，y轴的交点。曲线
的参数方程为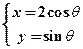
（
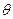为参数）。
（Ⅰ）求M,N的极坐标，并写出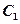的直角坐标方程；
（Ⅱ）求N点与曲线上的动点距离的最大值。
（本小题满分10分）
选修4-1：几何证明选讲
自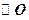
外一点p引切线与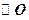切于点A，M为PA的中点，过M引割线交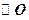于B、C两点。
求证：
（Ⅰ）
；
（Ⅱ）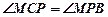
。