(1) 用辗转相除法求840与1 764的最大公约数.
(2)把“五进制”数 转化为“十进制”数,再把它转化为“八进制”数。
转化为“十进制”数,再把它转化为“八进制”数。
(本小题满分10分)某公司通过报纸和电视两种方式做销售某种商品的广告,根据统计资料,销售收入R(万元)与报纸广告费用x1(万元)及电视广告费用x2(万元)之间的关系有如下经验公式:R=-2x12-x22+13x1+11x2-28.
(1)若提供的广告费用共为5万元,求最优广告策略.(即收益最大的策略,其中收益=销售收入-广告费用)
(2)在广告费用不限的情况下,求最优广告策略
(本小题满分10分)已知函数f(x)= 的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
(本小题满分14分)已知函数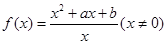 是奇函数,且满足
是奇函数,且满足
(1)求实数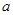 、
、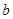 的值;
的值;
(2)试证明函数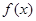 在区间
在区间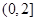 单调递减,在区间
单调递减,在区间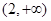 单调递增;
单调递增;
(3)是否存在实数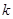 同时满足以下两个条件:
同时满足以下两个条件:
①不等式 对
对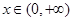 恒成立;②方程
恒成立;②方程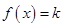 在
在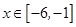 上有解.
上有解.
若存在,试求出实数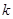 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分14分)某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
| 组号 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
| 分组 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;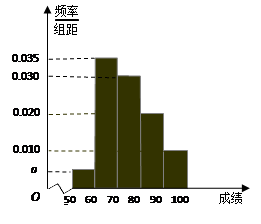
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
(本小题满分13分)设关于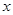 的一元二次方程
的一元二次方程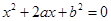 .
.
(1)若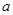 是从
是从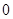 、
、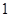 、
、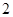 、
、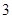 四个数中任取的一个数,
四个数中任取的一个数,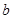 是从
是从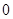 、
、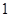 、
、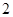 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若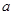 是从区间
是从区间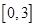 任取的一个数,
任取的一个数,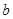 是从区间
是从区间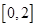 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.