记  , 若函数
, 若函数 .
.
(Ⅰ)用分段函数形式写出函数 的解析式;
的解析式;
(Ⅱ)求不等式 的解集.
的解集.
已知点(1,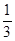 )是函数
)是函数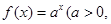 且
且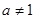 )的图象上一点,等比数列
)的图象上一点,等比数列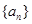 的前n项和为
的前n项和为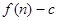 ,数列
,数列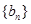
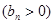 的首项为c,且前n项和
的首项为c,且前n项和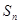 满足
满足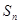 -
-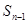 =
=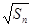 +
+ (n
(n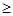 2).
2).
(1)求数列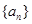 和
和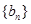 的通项公式;
的通项公式;
(2)若数列{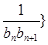 前n项和为
前n项和为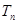 ,问
,问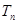 >
>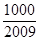 的最小正整数n是多少?
的最小正整数n是多少?
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.
在长方体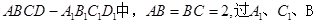 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为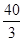 .
.
(1)求棱 的长;
的长;
(2)求经过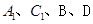 四点的球的表面积.
四点的球的表面积.
已知函数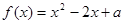 ,
,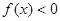 的解集为
的解集为
(1)求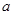 ,
,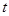 的值;
的值;
(2)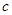 为何值时,
为何值时,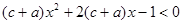 的解集为R.
的解集为R.
在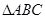 中,
中,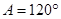 ,
,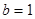 ,
, ,
,
求:(1) ,
, ;
;
(2)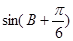 的值.
的值.