运用旋转矩阵,求直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程。
(本小题满分12分)如图是从上下底面处在水平状态下的棱长为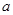 的正方体
的正方体 中分离出来的:
中分离出来的:
(1)试判断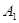 是否在平面
是否在平面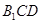 内;(回答是与否)
内;(回答是与否)
(2)求异面直线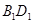 与
与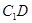 所成的角;
所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积
(本小题满分12分)如图,在直三棱柱 中,
中, ,
,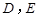 分 别是棱
分 别是棱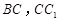 上的点(点
上的点(点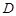 不同于点
不同于点 ),且
),且 为
为 的中点.
的中点.
求证:(1)平面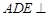 平面
平面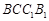 (2)直线
(2)直线 平面
平面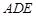
(本小题满分12分).已知幂函数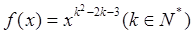 的图象关于
的图象关于 轴对称,且在区间
轴对称,且在区间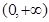 上是减函数,
上是减函数,
(1)求函数 的解析式;((2)若
的解析式;((2)若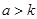 ,比较
,比较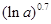 与
与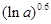 的大小;
的大小;
(本小题满分12分)设集合 ,
,
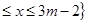 ,若
,若 ,求实数m的取值范围.
,求实数m的取值范围.
已知函数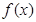 是定义在
是定义在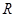 上的偶函数,已知当
上的偶函数,已知当 时,
时, .
.
(1)求函数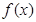 的解析式;
的解析式;
(2)求函数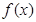 的单调递增区间;
的单调递增区间;
(3)求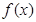 在区间
在区间 上的值域。
上的值域。