(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
如题(19)图,在四棱锥 中,
中,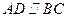 且
且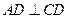 ;平面
;平面
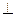 平面
平面 ,
, ;
; 为
为 的中点,
的中点,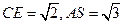 。求:
。求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角 的大小。
的大小。
各项均为正数的数列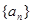 的前
的前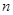 项和为
项和为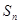 ,满足
,满足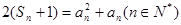 .
.
(1)求数列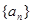 的通项公式;
的通项公式;
(2)若数列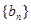 满足
满足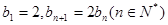 ,数列
,数列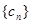 满足
满足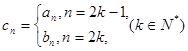 ,数列
,数列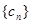 的前
的前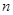 项和为
项和为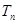 ,求
,求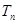 ;
;
(3)若数列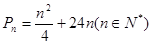 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的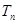 ,试图确定
,试图确定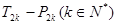 的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.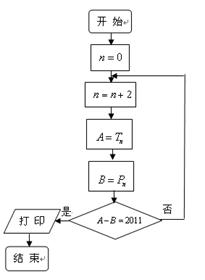
如图,在四棱锥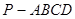 中,底面
中,底面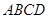 是矩形.已知
是矩形.已知 .
.
(1)证明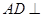 平面
平面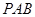 ;
;
(2)求异面直线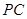 与
与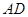 所成的角的大小;
所成的角的大小;
(3)求二面角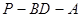 的大小.
的大小.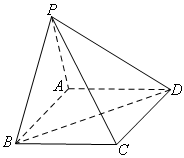
已知向量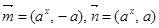 ,其中
,其中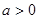 且
且 ,
,
(1)当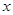 为何值时,
为何值时,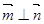 ;
;
(2)解关于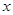 的不等式
的不等式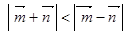 .
.
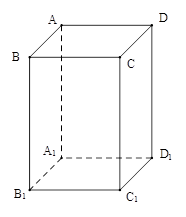
(理科)已知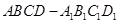 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,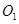 是
是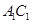 和
和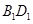 的交点.
的交点.
⑴设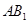 与底面
与底面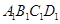 所成的角的大小为
所成的角的大小为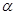 ,二面角
,二面角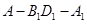 的大小为
的大小为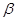 ,试确定
,试确定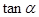 与
与 的一个等量关系,并给出证明;
的一个等量关系,并给出证明;
⑵若点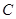 到平面
到平面 的距离为
的距离为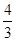 ,求正四棱柱
,求正四棱柱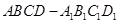 的高.
的高.
(文科)已知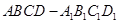 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高 .求:
.求:
⑵异面直线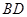 与
与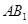 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);
⑵ 四面体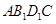 的体积.
的体积.