如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,已知AB=a,AC=2,

AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.
(Ⅰ)证明:BD⊥A1C;
(Ⅱ)若二面角B-A1D-B1的大小为60º,试求a的值.
某种报纸,进货商当天以每份进价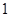 元从报社购进,以每份售价
元从报社购进,以每份售价 元售出。若当天卖不完,剩余报纸报社以每份
元售出。若当天卖不完,剩余报纸报社以每份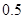 元的价格回收。根据市场统计,得到这个季节的日销售量
元的价格回收。根据市场统计,得到这个季节的日销售量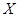 (单位:份)的频率分布直方图(如图所示),将频率视为概率。
(单位:份)的频率分布直方图(如图所示),将频率视为概率。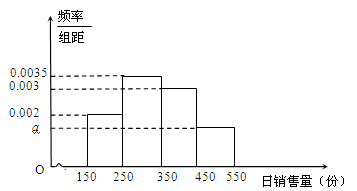
(Ⅰ)求频率分布直方图中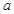 的值;
的值;
(Ⅱ)若进货量为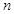 (单位:份),当
(单位:份),当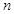

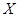 时,求利润
时,求利润 的表达式;
的表达式;
(Ⅲ)若当天进货量 ,求利润
,求利润 的分布列和数学期望
的分布列和数学期望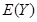 (统计方法中,同一组数据常用该组区间的中点值作为代表).
(统计方法中,同一组数据常用该组区间的中点值作为代表).
在 中,角
中,角 所对的边分别为
所对的边分别为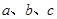 ,已知
,已知 ,
,
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,求
,求 的周长的取值范围.
的周长的取值范围.
设椭圆 的离心率
的离心率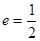 ,
,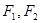 是其左右焦点,点
是其左右焦点,点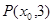 是直线
是直线 (其中
(其中 )上一点,且直线
)上一点,且直线 的倾斜角为
的倾斜角为 .
.
(Ⅰ)求椭圆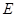 的方程;
的方程;
(Ⅱ)若 是椭圆
是椭圆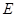 上两点,满足
上两点,满足 ,求
,求 (
( 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.
设函数 (Ⅰ)若函数
(Ⅰ)若函数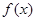 在
在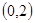 上单调递减,在区间
上单调递减,在区间 单调递增,求
单调递增,求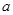 的值;
的值;
(Ⅱ)若函数 在
在 上有两个不同的极值点,求
上有两个不同的极值点,求 的取值范围;
的取值范围;
(Ⅲ)若方程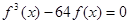 有且只有三个不同的实根,求
有且只有三个不同的实根,求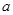 的取值范围。
的取值范围。
已知数列 的前n项和为
的前n项和为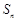 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,数列
,数列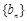 的前n项和为
的前n项和为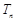 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.